EL CONJUNTO DE LOS NÚMEROS ENTEROS
EL CONJUNTO DE LOS NÚMEROS ENTEROS
REPRESENTACIÓN DE LOS NÚMEROS ENTEROS EN LA RECTA NUMÉRICA, COMPARACIÓN Y ORDEN
Z = {… ; - 3 ; - 2 ; - 1 ; 0 ; 1 : 2 : 3 : …}
La recta numérica para los números enteros:
A todo número entero le corresponde un punto en la recta numérica entera, recíprocamente, a todo punto de la recta numérica entera le corresponde un número entero.
El número cero no tiene signo.
Hacia la izquierda de cero (0) encontramos los números enteros negativos, hasta el menos infinito (- ∞).
Hacia la derecha de cero (0) encontramos los números enteros positivos, hasta el más infinito (+ ∞).
COMPARACIÓN DE NÚMEROS ENTEROS
LEY DE TRICOTOMIA
Dados dos números enteros a y b se cumple solamente una de las siguientes afirmaciones:
a < b ; a > b ; a = b
Si dos números se encuentran ubicados en la recta numérica, es mayor el número que se encuentra a la derecha y es menor el número que se encuentra a la izquierda.
Ejemplo:
Comparamos en la recta numérica los números – 5 y – 2.
Interpretamos según el gráfico:
Si leemos de izquierda a derecha, – 5 es menor que – 2.
Simbólicamente – 5 < – 2
Si leemos de derecha a izquierda, – 2 es mayor que – 5.
Simbólicamente – 2 > – 5
La comparación también se puede realizar sin utilizar la recta numérica.
El orden de los números enteros se realiza de dos formas: ascendente y descendente.
Ascendente. - Al ordenar números enteros en forma ascendente o creciente se realiza del menor número al mayor.
Descendente. - Al ordenar números enteros en forma descendente o decreciente se realiza del mayor número al menor.
Ejemplos:
En un problema sobre temperatura ambiental se formulan las siguientes preguntas.
1) Ordena en forma ascendente las siguientes temperaturas:
1 ; - 3 ; 6; - 1 ; 0 y 12 ° C
2) Ordena en forma descendente las siguientes temperaturas:
- 2 ; 6 ; 12 ; 0 ; - 1 y 9 ° C
Los números enteros en la recta numérica, comparación y orden
Problema:
En una comunidad andina, un día desde las 0:00 horas hasta las 12:00 horas, cada 2 horas, se registran las siguientes temperaturas ambientales, observa la tabla:
A partir de la información responde las siguientes preguntas:
1) Representa en la recta numérica para los números enteros el registro de la temperatura y hora.
2) ¿Cuánto es la temperatura mayor y cuánto la menor?
ü La temperatura mayor es 12 °C.
ü La temperatura menor es - 3 °C
3) ¿Cuántos registros de temperatura están a grados Celsius sobre cero?. Escribe la hora de registro y la temperatura.
5 registros de temperatura están a grados Celsius sobre cero:
04:00 h a 1 °C.
06:00 h a 4 °C.
08:00 h a 6 °C.
10:00 h a 9 °C.
12:00 h a 12 °C.
4) ¿Cuántos registros de temperatura están a grados Celsius bajo cero?. Escribe la hora de registro y la temperatura.
2 registros de temperatura están a grados Celsius bajo cero:
02:00 h a - 1 °C.
00:00 h a - 3 °C.
5) ¿Cuánto es la variación de temperatura desde las 04:00 h hasta las 12:00 h?. ¿La temperatura aumenta o disminuye, en cuántos grados Celsius?.
12 – 1 = 11 °C
ü La variación de la temperatura es de 11 °C.
ü La temperatura aumenta en 11 °C.
6) ¿Cuánto es la variación de temperatura desde las 00:00 h hasta las 02:00 h?. ¿La temperatura aumenta o disminuye, en cuántos grados Celsius?.
– 1 – (– 3 ) = – 1 + 3 = 2 °C
ü La variación de la temperatura es de 2 °C.
ü La temperatura aumenta en 2 °C.
7) ¿Cuánto es la variación de temperatura desde las 02:00 h hasta las 10:00 h?. ¿La temperatura aumenta o disminuye, en cuántos grados Celsius?.
9 – (– 1 ) = 9 + 1 = 10 °C
ü La variación de la temperatura es de 10 °C.
ü La temperatura aumenta en 10 °C.
8) Comparación de temperaturas:
Escribe en los recuadros > ; < o =.
9) Ordena en forma ascendente las siguientes temperaturas:
1 ; - 3 ; 6; - 1 ; 0 y 12 ° C
10) Ordena en forma descendente las siguientes temperaturas:
- 2 ; 6 ; 12 ; 0 ; - 1 y 9 ° C
Vídeo.
Los números enteros en la recta numérica comparación y orden: https://youtu.be/fDHoLW_zkm4
ADICIÓN Y SUSTRACCIÓN DE NÚMEROS ENTEROS
ADICIÓN DE NÚMEROS ENTEROS
12 es sumando.
15 es sumando.
27 es el resultado o suma
AXIOMAS Y TEOREMAS DE LA ADICIÓN DE NÚMEROS ENTEROS
A) AXIOMA DE CLAUSURA
Al sumar dos números enteros se obtiene como suma otro número entero
Si: a Є Z y b Є Z → (a + b) Є Z
Ejemplo:
3 Є Z
9 Є Z
3 + 9 = 12
12 Є Z
B) AXIOMA DE CONMUTATIVIDAD
Si cambiamos el orden de los sumandos la suma no se altera
a + b = b + a
Ejemplo:
3 + 7 = 7 + 3
10 = 10
C) AXIOMA DE ASOCIATIVIDAD
Si asociamos los sumandos de diferente forma la suma no se altera
(a + b) + c = a + (b + c)
Ejemplo:
(5 + 7) + 4 = 5 + (7 + 4)
(12) + 4 = 5 + (11)
12 + 4 = 5 + 11
16 = 16
D) AXIOMA DE ELEMENTO NEUTRO O IDENTIDAD ADITIVA
El elemento neutro aditivo es el número “0”, es decir, si a cualquier número entero le sumamos cero “0” la suma es el mismo número entero
a + 0 = 0 + a = a
Ejemplo:
25 + 0 = 0 + 25 = 25
E) AXIOMA DE INVERSO ADITIVO
Si a un número entero le sumamos su inverso el resultado es cero.
a + (- a) = 0
Ejemplo:
9 + (- 9) = = 0
SUSTRACCIÓN DE NÚMEROS ENTEROS
7 es el minuendo.
12 es el sustraendo.
- 5 es la diferencia.
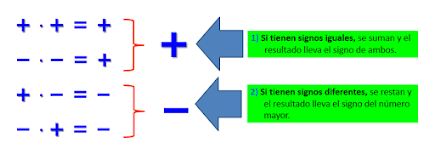
REGLAS PARA LA ADICIÓN Y SUSTRACCIÓN DE NÚMEROS ENTEROS:
REGLA Nro. 1
Si los números tienen igual signo, se suman y el resultado lleva el signo de ambos.
Ejemplos:
1) + 14 + 11 = + 25
2) – 5 – 9 = – 14
REGLA Nro. 2
Si los números tienen signo diferente, se restan y el resultado lleva el signo del número mayor.
Ejemplos:
1) + 7 – 10 = – 3
2) – 4 + 15 = + 11
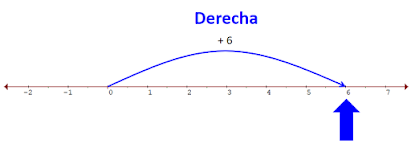
LOS NÚMEROS ENTEROS EN LA RECTA NUMÉRICA
Los números enteros en la recta numérica son distancias desde cero (0) al número.
Si el número lleva el signo (+) o es positivo, la distancia es desde cero (0) hacia la derecha.
Si el número lleva el signo (-) o es negativo, la distancia es desde cero (0) hacia la izquierda.
Ejemplos:
1) + 6
Expresamos la distancia con valor absoluto: | + 6 | = 6
Expresamos la distancia con valor absoluto: | – 5 | = 5
Suma y resta de números enteros en la recta numérica y aplicando reglas
Resuelve:
1) + 1 + 6 = + 7
Primera forma – En la recta numérica
Segunda forma – Aplicando reglas
1) Si tienen signos iguales, se suman y el resultado lleva el signo de ambos.
+ 1 y + 6 tienen el mismo signo, se suman 1 + 6 = 7 y el resultado lleva el signo de ambos + 7
+ 1 + 6 = + 7
2) – 2 – 4 = – 6
Primera forma – En la recta numérica
– 2 – 4 = – 6
3) + 6 – 9 = – 3
Primera forma – En la recta numérica
Segunda forma – Aplicando reglas
2) Si tienen signos diferentes, se resta y el resultado lleva el signo de la cantidad mayor.
+ 6 y – 9 tienen signos diferentes, se restan 9 – 6 = 3 y el resultado lleva el signo del número mayor, sin considerar el signo. El número mayor es 9 y tiene signo – , por tanto, el resultado es – 3
+ 6 – 9 = – 3
4) – 6 + 10 = + 4
Primera forma – En la recta numérica
Segunda forma – Aplicando reglas
2) Si tienen signos diferentes, se resta y el resultado lleva el signo de la cantidad mayor.
– 6 y + 10 tienen signos diferentes, se restan 10 – 6 = 4 y el resultado lleva el signo del número mayor, sin considerar el signo. El número mayor es 10 y tiene signo + , por tanto, el resultado es + 4.
– 6 + 10 = + 4
Vídeo.
Suma y resta de números enteros con paréntesis, corchetes y llaves
Al resolver la suma y resta de números enteros con signos de agrupación: paréntesis, corchetes y llaves, se debe eliminar los signos de agrupación en el siguiente orden:
1) Paréntesis.
2) Corchetes.
3) Llaves.
Se presentan dos casos.
CASO 1: Si el signo que le antecede al signo de agrupación es (+), se elimina el signo de agrupación y el número que se encuentra dentro se copia con su mismo signo.
Ejemplo:
1) + ( - 5) = - 5
Como a los paréntesis le antecede el signo (+), se eliminan los paréntesis y el número que se encuentra dentro mantiene su signo, es decir, se copia como tal, - 5.
CASO 2: Si el signo que le antecede al signo de agrupación es (-), se elimina el signo de agrupación y el número que se encuentra dentro cambia de signo.
Ejemplo:
2) - ( - 7) = + 7
Como a los paréntesis le antecede el signo (-), se eliminan los paréntesis y el número que se encuentra dentro cambia de signo, + 7.
Ejemplo: Resuelve.
- 5 + {4 - [- 3 + (6 – 9 )]- 2} – 7
Solución:
- 5 + {4 - [- 3 + (6 – 9 )]- 2} – 7
Eliminamos paréntesis, como le antecede el signo ( + ), se copian los números con su signo + 6 – 9.
- 5 + {4 - [- 3 + 6 – 9 ]- 2} – 7
- 5 + {4 - [- 3 + 6 – 9 ]- 2} – 7
Eliminamos corchetes, como le antecede el signo ( - ), los números cambian de signo + 3 – 6 + 9.
- 5 + {4 + 3 - 6 + 9 - 2} – 7
- 5 + {4 + 3 - 6 + 9 - 2} – 7
Eliminamos llaves, como le antecede el signo ( + ), se copian lo números con su signo + 4 + 3 – 6 + 9 – 2.
- 5 + 4 + 3 - 6 + 9 - 2 – 7
Sumamos los números que tienen el signo (+).
+ 4 + 3 + 9 = + 16
Sumamos los números que tienen el signo (-).
– 5 – 6 – 2 – 7 = – 20
Se tiene:
+ 16 – 20
Como tienen signos diferentes se resta 20 – 16 = 4
El resultado lleva el signo de la cantidad mayor, la cantidad mayor es 20 y tiene signo (-).
Por tanto, el resultado es negativo
Respuesta: – 4
Vídeo:
Suma y resta de números enteros con paréntesis corchetes y llaves: https://youtu.be/wscsCqH2O2E
Suma y resta de números enteros con paréntesis
Al resolver la suma y resta de números enteros con signos de agrupación: paréntesis, corchetes y llaves, se debe eliminar los signos de agrupación en el siguiente orden:
1) Paréntesis.
2) Corchetes.
3) Llaves.
Se presentan dos casos.
CASO 1:
Si el signo que le antecede al signo de agrupación es (+), se elimina el signo de agrupación y el número que se encuentra dentro se copia con su mismo signo.
Ejemplo:
1) + ( - 5) = - 5
Como a los paréntesis le antecede el signo (+), se eliminan los paréntesis y el número que se encuentra dentro mantiene su signo, es decir, se copia como tal, - 5.
CASO 2:
Si el signo que le antecede al signo de agrupación es (-), se elimina el signo de agrupación y el número que se encuentra dentro cambia de signo.
Ejemplo:
2) - ( - 7) = + 7
Como a los paréntesis le antecede el signo (-), se eliminan los paréntesis y el número que se encuentra dentro cambia de signo, + 7.
Resuelve:
– 5 + ( – 4 ) – (2 – 5) – (– 1) – 4
Solución:
– 5 + ( – 4 ) – (2 – 5) – (– 1) – 4
Eliminamos el primer paréntesis + ( - 4).
Como le antecede el signo ( + ), se copia el número con si signo: – 4 .
Eliminamos el segundo paréntesis - ( 2 - 5).
Como le antecede el signo ( - ), los números cambian de signo: - 2 + 5.
Eliminamos el tercer paréntesis - ( - 1).
Como le antecede el signo ( - ), el número cambia de signo: + 1.
Nos queda:
- 5 – 4 – 2 + 5 + 1 – 4
Sumamos los números que tienen el signo (+).
+ 5 + 1 = + 6
Sumamos los números que tienen el signo (-).
– 5 – 4 – 2 – 4 = – 15
Se tiene:
+ 6 – 15
Como tienen signos diferentes se resta 15 – 6 = 9
El resultado lleva el signo de la cantidad mayor, la cantidad mayor es 15 y tiene signo (-).
Por tanto, el resultado es negativo
Respuesta: – 9
Vídeo:
Suma y resta de números enteros con paréntesis: https://youtu.be/_CjLb2xlJeo
MULTIPLICACIÓN DE NÚMEROS ENTEROS
LEY DE SIGNOS PARA LA MULTIPLICACIÓN DE NÚMEROS ENTEROS
AXIOMAS Y TEOREMAS DE LA MULTIPLICACIÓN DE NÚMEROS ENTEROS
A) AXIOMA DE CLAUSURA
Si multiplicamos dos números enteros cualesquiera, el producto o resultado es otro número entero
Si: a Є Z y b Є Z → (a . b) Є Z
Ejemplo:
– 3 Є Z
+ 7 Є Z
– 3 x + 7 = – 21
– 21 Є Z
B) AXIOMA DE CONMUTATIVIDAD
Si cambiamos el orden de los factores el producto es el mismo
a · b = b · a
Ejemplo:
3 x – 5 = – 5 x 3
C) AXIOMA DE ASOCIATIVIDAD
Si asociamos de modo diferente los factores el producto es el mismo
a (b · c) = (a · b) c
Ejemplo:
– 5 ( – 3 x +7) = (– 5 x – 3) x + 7
– 5 ( – 21) = (+ 15) x + 7
+ 105 = + 105
D) AXIOMA DE ELEMENTO NEUTRO
El número uno “1” es el elemento neutro multiplicativo, es decir si multiplicamos cualquier número entero por uno “1”, el resultado o producto siempre es el mismo número entero
a · 1 = 1 · a = a
Ejemplo:
– 3 x 1 = 1 x – 3 = – 3
E) TEOREMA DE MONOTONIA
Si a ambos miembros de una igualdad multiplicamos por un mismo número la igualdad se mantiene
Si: a = b → a · c = b · c
F) TEOREMA DEL ELEMENTO ABSORVENTE
Si multiplicamos un número por cero “0” el resultado o producto siempre es cero “0”
a . 0 = 0 . a = 0
Ejemplo:
– 7 x 0 = 1 x – 7 = 0
G) AXIOMA DE DISTRIBUTIVIDAD DE LA MULTIPLICACIÓN CON RESPECTO A LA ADICIÓN
a (b + c) = ab + ac
Ejemplo:
– 7 ( 3 + – 4) = – 7 x 3 + – 7 x – 4 = – 21 + 28 = + 7
H) AXIOMA DE DISTRIBUTIVIDAD DE LA MULTIPLICACIÓN CON RESPECTO A LA SUSTRACCIÓN
a (b - c) = ab – ac
Ejemplo:
5 ( 6 – 4) = 5 x 6 – 5 x 4 = 30 – 20 = 10
Multiplicación de números enteros – Ley de signos para la multiplicación
Al multiplicar números enteros primero se multiplican los signos, aplicando la ley de signos para la multiplicación. Luego se multiplican los números.
Ley de signos para la multiplicación
Ejemplos:
1) (+ 5 ) (– 9 ) =
Primero multiplicamos los signos + por – es igual a – .
Luego multiplicamos 5 x 9 = 45.
El resultado – 45.
(+ 5 ) (– 9 ) = – 45
2) (+ 3 ) (+ 8 ) =
Primero multiplicamos los signos + por + es igual a + .
Luego multiplicamos 3 x 8 = 24.
El resultado + 24.
(+ 3 ) (+ 8 ) = + 24
3) (– 7 ) (+ 10 ) =
Primero multiplicamos los signos – por + es igual a – .
Luego multiplicamos 7 x 10 = 70.
El resultado – 70.
(– 7 ) (+ 10 ) = – 70
4) (– 5 ) (– 8 ) =
Primero multiplicamos los signos – por – es igual a + .
Luego multiplicamos 5 x 8 = 40.
El resultado + 40.
(– 5 ) (– 8 ) = + 40
Ejemplos:
1) (+ 4 ) (– 12 ) = - 48
2) (– 8 ) ( + 9 ) = - 72
3) (+ 5 ) ( + 11 ) = + 55
4) (– 7 ) (– 9 ) = + 63
Vídeo:
Multiplicación de números enteros: https://youtu.be/3eHO2wxpWEk
División de números enteros – Ley de signos para la división
Al dividir números enteros primero se dividen los signos, aplicando la ley de signos para la división. Luego se dividen los números.
Ley de signos para la división
Ejemplos:
1) (+ 55 ) ÷ (– 11 )
Dividimos los signos + entre – es igual a –.
Dividimos 55 ÷11= 5.
El resultado – 5.
(+ 55 ) ÷ (– 11 ) = – 5
2) (– 90 ) ÷ (– 10 )
Dividimos los signos – entre – es igual a +.
Dividimos 90 ÷10 = 9.
El resultado + 9.
(+ 55 ) ÷ (– 11 ) = – 5
3) (+ 49 ) ÷ (+ 7 )
Dividimos los signos + entre + es igual a +.
Dividimos 49 ÷ 7 = 7.
El resultado + 7.
(+ 49 ) ÷ (+ 7 ) = + 7
4) (– 100 ) ÷ (+ 25 )
Dividimos los signos – entre + es igual a –.
Dividimos 100 ÷ 25 = 4.
El resultado – 4.
(– 100 ) ÷ (+ 25 ) = – 4
Ejemplos:
1) (+ 24 ) ÷ (– 6 ) = - 4
2) (– 30 ) ÷ ( + 5 ) = - 6
3) (+ 72 ) ÷ ( + 8 ) = + 9
4) (– 63 ) ÷ (– 9 ) = + 7
Vídeo:
División de números enteros: https://youtu.be/IgocJO-Wpc4
Multiplicación de tres o más números enteros
1) Se multiplican los signos de los factores aplicando la ley de signos.
2) Se multiplican los números
Resumen 1:
Si el número de veces que aparece el signo negativo ( – ) es par, el resultado es positivo ( + ).
Resumen 2:
Si el número de veces que aparece el signo negativo ( – ) es impar, el resultado es negativo ( – ).
Ejemplos: Resuelve.
1) (+ 4 ) (– 5 ) (– 3)
Multiplicamos los signos + · – · – = +
Multiplicamos 4 · 5 · 3 = 60
Resultado final: + 60
(+ 4 ) (– 5 ) (– 3) = + 60
2) (– 8 ) ( + 9 )(+ 2) =
Multiplicamos los signos – · + · – = –
Multiplicamos 8 · 9 · 2 = 144
Resultado final: – 144
(– 8 ) ( + 9 )(+ 2) = – 144
3) (– 5 ) (– 6 )(– 7)(– 3) =
Multiplicamos los signos – · – · – · – = +
Multiplicamos 5 · 6 · 7 · 3 = 630
Resultado final: + 630
(– 5 ) (– 6 )(– 7)(– 3) = + 630
4) (– 2 ) (+ 3 )(– 4)(+ 5)(– 1) =
Multiplicamos los signos – · + · – · + · – = –
Multiplicamos 2 · 3 · 4 · 5 · 1 = 120
Resultado final: – 120
(– 2 ) (+ 3 )(– 4)(+ 5)(– 1) = – 120
Vídeo:
Multiplicación de tres o más números enteros: https://youtu.be/QgVGUAmM298
Potenciación de números enteros
La potenciación es una multiplicación de un mismo factor en un número limitado de veces.
Ejemplos:
1) (– 3)3 =
La base es – 3 y el exponente 3.
El exponente 3 nos indica que la base – 3 se debe multiplicar 3 veces.
(– 3) (– 3) (– 3)
Multiplicamos los signos – x – x – = –
Multiplicamos los números 3 x 3 x 3 = 27
El resultado final: – 27
(– 3)3 = (– 3) (– 3) (– 3) = – 27
2) (– 2)4 =
La base es – 2 y el exponente 4.
El exponente 4 nos indica que la base – 2 se debe multiplicar 4 veces.
(– 2) (– 2) (– 2) (– 2)
Multiplicamos los signos – x – x – x – = +
Multiplicamos los números 2 x 2 x 2 x 2 = 16
El resultado final: + 16
(– 2)4 = (– 2) (– 2) (– 2) (– 2) = + 16
3) (+ 5)4 =
La base es + 5 y el exponente 4.
El exponente 4 nos indica que la base + 5 se debe multiplicar 4 veces.
(+ 5) (+ 5) (+ 5) (+ 5)
Multiplicamos los signos + x + x + x + = +
Multiplicamos los números 5 x 5 x 5 x 5 = 625
El resultado final: + 625
(+ 5)4 = (+ 5) (+ 5) (+ 5) (+ 5) = + 625
4) (+ 3)5 =
La base es + 3 y el exponente 5.
El exponente 5 nos indica que la base + 3 se debe multiplicar 5 veces.
(+ 3) (+ 3) (+ 3) (+ 3) (+ 3)
Multiplicamos los signos + x + x + x + x + = +
Multiplicamos los números 3 x 3 x 3 x 3 x 3 = 243
El resultado final: + 243
(+ 3)5 = (+ 3) (+ 3) (+ 3) (+ 3) (+ 3) = + 243
Vídeo:
Potenciación de números enteros: https://youtu.be/oRkCPPa5ZtE
Potenciación de números negativos: exponente par e impar
Caso 1: Todo número negativo elevado a un exponente par, su resultado es positivo.
Caso 2: Todo número negativo elevado a un exponente impar, su resultado es negativo.
Si la base de la potencia es positiva, el exponente puede ser par o impar, el resultado siempre es positivo
Ejemplos:
1) (– 3)4 =
La base es – 3 y el exponente 4.
El exponente 4 nos indica que la base – 3 se debe multiplicar 4 veces.
(– 3) (– 3) (– 3) (– 3)
Multiplicamos los signos – x – x – x – = +
Multiplicamos los números 3 x 3 x 3 x 3 = 81
El resultado final: + 81
(– 3)4 = (– 3) (– 3) (– 3) (– 3) = + 81
2) (– 5)2 =
La base es – 5 y el exponente 2.
El exponente 2 nos indica que la base – 5 se debe multiplicar 2 veces.
(– 5) (– 5)
Multiplicamos los signos – x – = +
Multiplicamos los números 5 x 5 = 25
El resultado final: + 25
(– 5)2 = (– 5) (– 5) = + 25
3) (– 2)5 =
La base es – 2 y el exponente 5.
El exponente 5 nos indica que la base – 2 se debe multiplicar 5 veces.
(– 2) (– 2) (– 2) (– 2) (– 2)
Multiplicamos los signos – x – x – x – x – = –
Multiplicamos los números 2 x 2 x 2 x 2 x 2 = 32
El resultado final: – 32
(– 2)5 = (– 2) (– 2) (– 2) (– 2) (– 2) = – 32
4) (– 4)3 =
La base es – 4 y el exponente 3.
El exponente 3 nos indica que la base – 4 se debe multiplicar 3 veces.
(– 4) (– 4) (– 4)
Multiplicamos los signos – x – x – = –
Multiplicamos los números 4 x 4 x 4 = 64
El resultado final: – 64
(– 4)3 = (– 4) (– 4) (– 4) = – 64
Vídeo:
Potenciación de números negativos exponente par e impar.
Sugerido para usted:
Vídeos de operaciones con números enteros: https://cutt.ly/8nTV3tS
Blog de números enteros completo: https://cutt.ly/inFZgHN
Vídeos de matemática en YouTube: https://cutt.ly/cnFLO6f